Computational Fluid Dynamics: Principles and Applications

CFD Book Das Ziel dieses englischsprachigen Buches, das nun in dritter aktualisierter und erweiterter Auflage vorliegt, ist es, Universitätsstudenten eine solide Grundlage für das Verständnis von numerischen Methoden zu vermitteln, die heute bei der computergestützten Strömungssimulation (CFD) eingesetzt werden. Darüber hinaus bietet es den Studierenden auch die Möglichkeit, praktische Erfahrungen in der Programmierung moderner CFD Software zu gewinnen. Das Buch richtet sich ebenfalls an Ingenieure und Wissenschaftler, die sich in das Gebiet der numerischen Strömungssimulation vertiefen wollen, sowie an solche, die CFD Programme entweder entwickeln oder anwenden. Dank des sehr detaillierten Stichwortverzeichnisses eignet es sich außerdem hervorragend als Referenzhandbuch. Jedes Kapitel enthält ein umfangreiches Literaturverzeichnis, welches eine ausgezeichnete Basis für das weitere Studium der Materie bietet.

Eine begleitende Webseite von Elsevier Science bietet Quellcodes in Fortran90 und in C++ für ein- sowie zweidimensionale Euler und Navier-Stokes Lösungsverfahren auf strukturieren, wie auch auf unstrukturierten Netzen. Dazu passende Programme für die Netzgenerierung befinden sich ebenfalls dort. Die Programme sind relativ einfach gehalten und sind gut dokumentiert. Sie erlauben es aber dennoch eine Vielzahl sehr unterschiedlicher Strömungsprobleme zu rechnen - angefangen von Düsenströmungen, über Profile bei verschiedenen Machzahlen, Turbinenschaufeln, bis zu Feststoffraketentriebwerken. Einige Simulationsergebnisse sind hier wiedergegeben. Zur Verfügung gestellt werden weiterhin auch Werkzeuge für die von Neumann'sche Stabilitätsanalyse von eindimensionalen Modellgleichungen, sowie Beispiele für die Parallelisierung von Simulationsprogrammen.

Für eine Bestellung siehe die Informationen am Ende der Seite. Liste mit Textkorrekturen sowie verbesserte Versionen der Beispielprogramme finden Sie auf der nächsten Seite. Um den Autor zu kontaktieren, schreiben Sie bitte an: info@cfd-ca.de.

CFD Book Chinese

Verfügbar ist ebenfalls eine Übersetzung der dritten Ausgabe ins Chinesische. Es kann unter dem folgenden Link bestellt werden.

Inhalt:

Acknowledgments
List of Symbols
Abbreviations

1 Introduction

2 Governing Equations
   2.1 The Flow and its Mathematical Description
   2.2 Conservation Laws
   2.3 Viscous Stresses
   2.4 Complete System of the Navier-Stokes Equations

3 Principles of Solution of the Governing Equations
   3.1 Spatial Discretization
   3.2 Temporal Discretization
   3.3 Turbulence Modeling
   3.4 Initial and Boundary Conditions

4 Structured Finite Volume Schemes
   4.1 Geometrical Quantities of a Control Volume
   4.2 General Discretization Methodologies
   4.3 Discretization of the Convective Fluxes
   4.4 Discretization of the Viscous Fluxes

5 Unstructured Finite Volume Schemes
   5.1 Geometrical Quantities of a Control Volume
   5.2 General Discretization Methodologies
   5.3 Discretization of the Convective Fluxes
   5.4 Discretization of the Viscous Fluxes

6 Temporal Discretization
   6.1 Explicit Time-Stepping Schemes
   6.2 Implicit Time-Stepping Schemes
   6.3 Methodologies for Unsteady Flows

7 Turbulence Modeling
   7.1 Basic Equations of Turbulence
   7.2 First-Order Closures
   7.3 Large-Eddy Simulation

8 Boundary Conditions
   8.1 Concept of Dummy Cells
   8.2 Solid Wall
   8.3 Far-Field
   8.4 Inlet/Outlet Boundary
   8.5 Injection Boundary
   8.6 Symmetry Plane
   8.7 Coordinate Cut
   8.8 Periodic Boundaries
   8.9 Interface Between Grid Blocks
   8.10 Flow Gradients at Boundaries of Unstructured Grids

9 Acceleration Techniques
   9.1 Local Time-Stepping
   9.2 Enthalpy Damping
   9.3 Residual Smoothing
   9.4 Multigrid
   9.5 Preconditioning for Low Mach Numbers
   9.6 Parallelization

10 Consistency, Accuracy and Stability
   10.1 Consistency Requirements
   10.2 Accuracy of Discretization Scheme
   10.3 Von Neumann Stability Analysis

11 Principles of Grid Generation
   11.1 Structured Grids
   11.2 Unstructured Grids

12 Software Applications
   12.1 Programs for Stability Analysis
   12.2 Structured 1-D Grid Generator
   12.3 Structured 2-D Grid Generators
   12.4 Structured to Unstructured Grid Converter
   12.5 Quasi 1-D Euler Solver
   12.6 Structured 2-D Euler/Navier-Stokes Solver
   12.7 Unstructured 2-D Euler/Navier-Stokes Solver
   12.8 Parallelization

A Appendix
   A.1 Governing Equations in Differential Form
   A.2 Quasilinear Form of the Euler Equations
   A.3 Mathematical Character of the Governing Equations
   A.4 Navier-Stokes Equations in Rotating Frame of Reference
   A.5 Navier-Stokes Equations Formulated for Moving Grids
   A.6 Thin Shear Layer Approximation
   A.7 Parabolized Navier-Stokes Equations
   A.8 Axisymmetric Form of the Navier-Stokes Equations
   A.9 Convective Flux Jacobian
   A.10 Viscous Flux Jacobian
   A.11 Transformation from Conservative to Characteristic Variables
   A.12 GMRES Algorithm
   A.13 Tensor Notation

Index

Titel: Computational Fluid Dynamics: Principles and Applications (3. Auflage)
Autor: Dr.-Ing. J. Blazek
Verlag: Elsevier Science Ltd. (www.elsevier.com)
Erschienen: März 2015
Form: Hartumschlag, 466 Seiten
ISBN: 978-0-08-099995-1

Siehe die Webseite zum Buch bei Elsevier Science, wo sich auch der Link zum Herunterladen der Beispielprogramme befindet. Dort kann das Buch auch bequem bestellt werden.

Beispielergebnisse der 2-d Strömungslöser

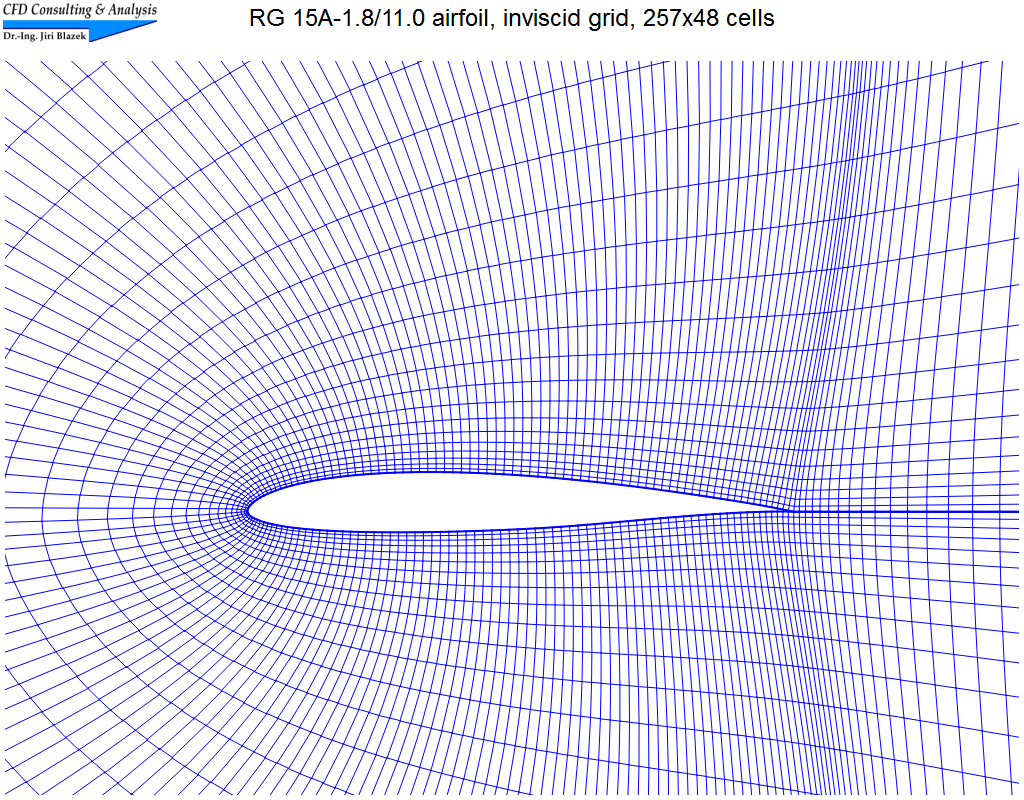
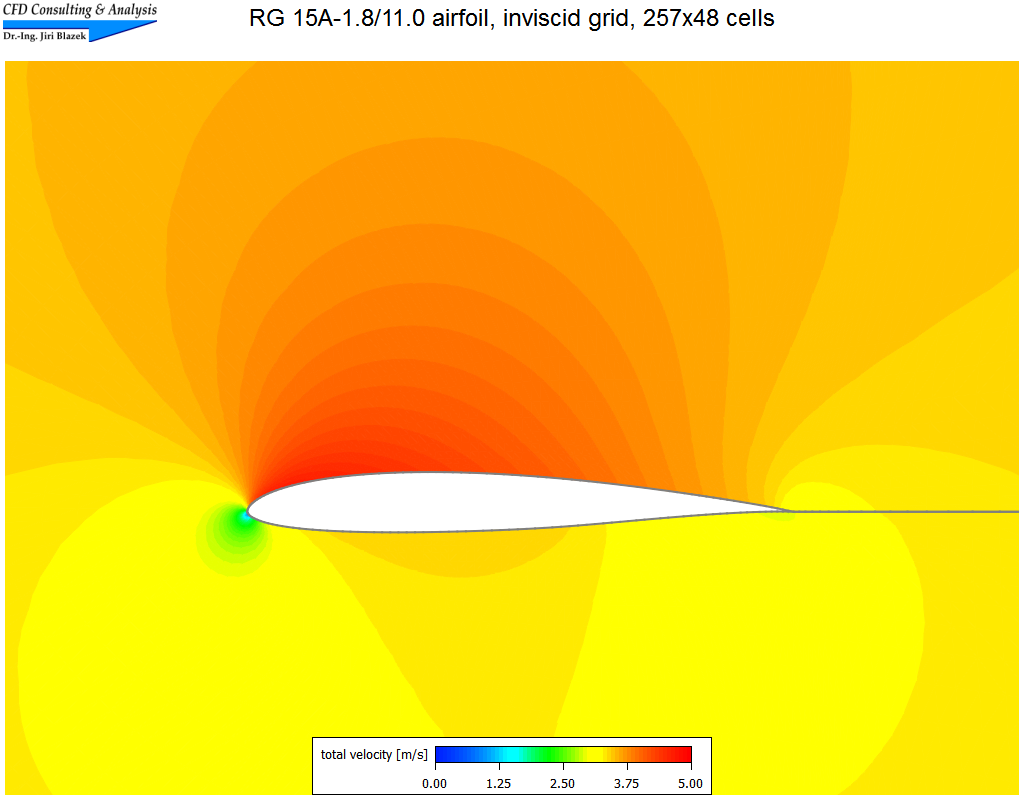
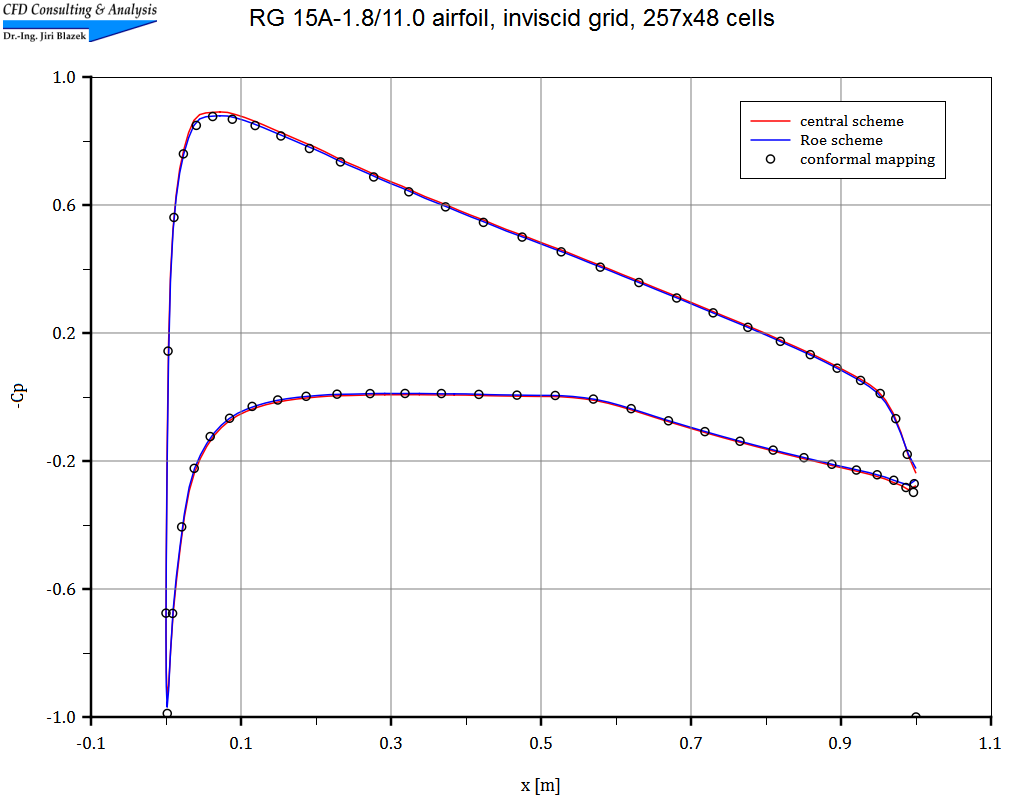
1. Unterschallströmung um das RG 15A-1.8/11.0 Profil

Die nahezu inkompressible Strömung (Machzahl=0.01, α=2°) wurde auf strukturiertem Netz (C-Typ) mit 257x48 Zellen mit Hilfe des zentralen, wie auch des upwind Schemas von Roe simuliert. Die Bilder zeigen einen Ausschnitt des Netzes, Isolinien der Gesamtgeschwindigkeit, sowie einen Vergleich der Druckkoeffizienten.

Zum Vergrößern anklicken

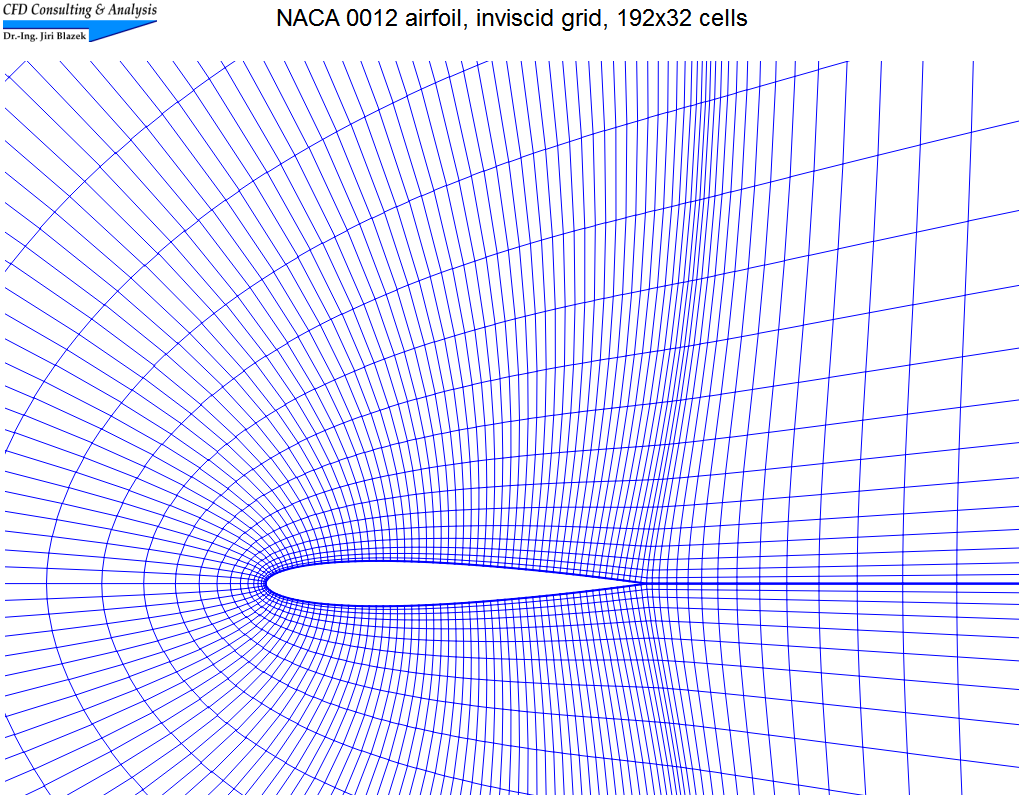
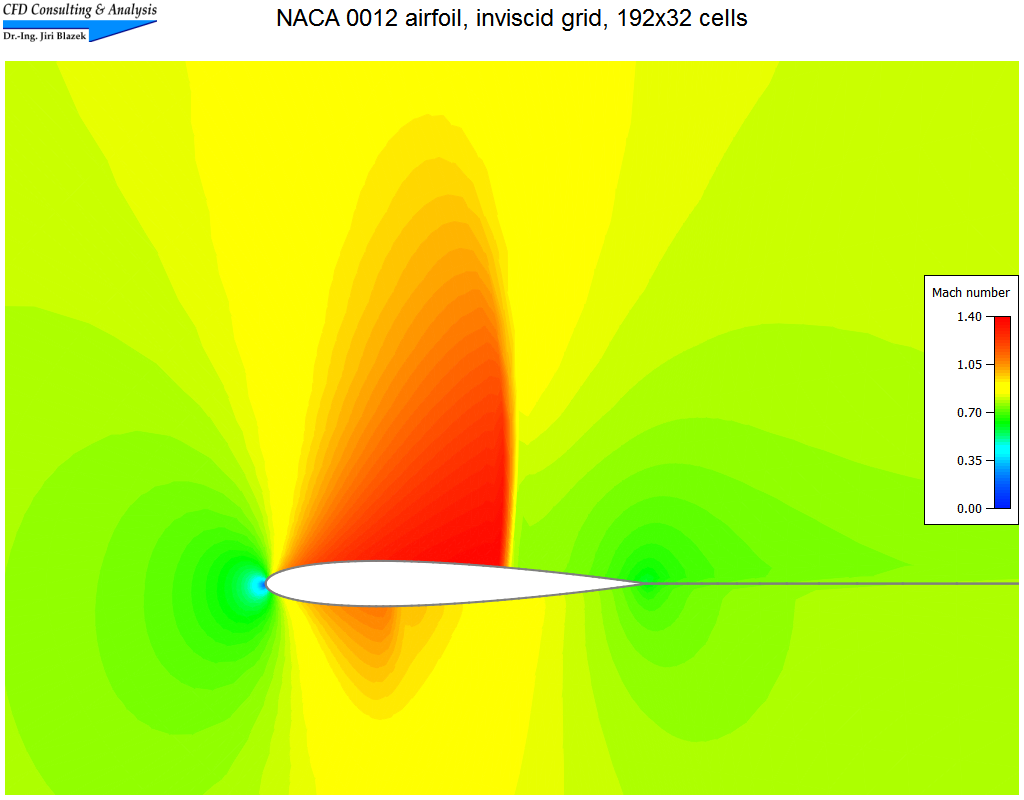
2. Transsonische Strömung um das NACA 0012 Profil

Die transsoniche Strömung (Machzahl=0.8, α=1.2°) wurde auf strukturiertem Netz (C-Typ) mit 192x32 Zellen mit Hilfe des zentralen, wie auch des upwind Schemas von Roe simuliert. Die Bilder zeigen einen Ausschnitt des Netzes, Isolinien der Machzahl, sowie einen Vergleich der Machzahlen entlang der Profilkontur.

Zum Vergrößern anklicken

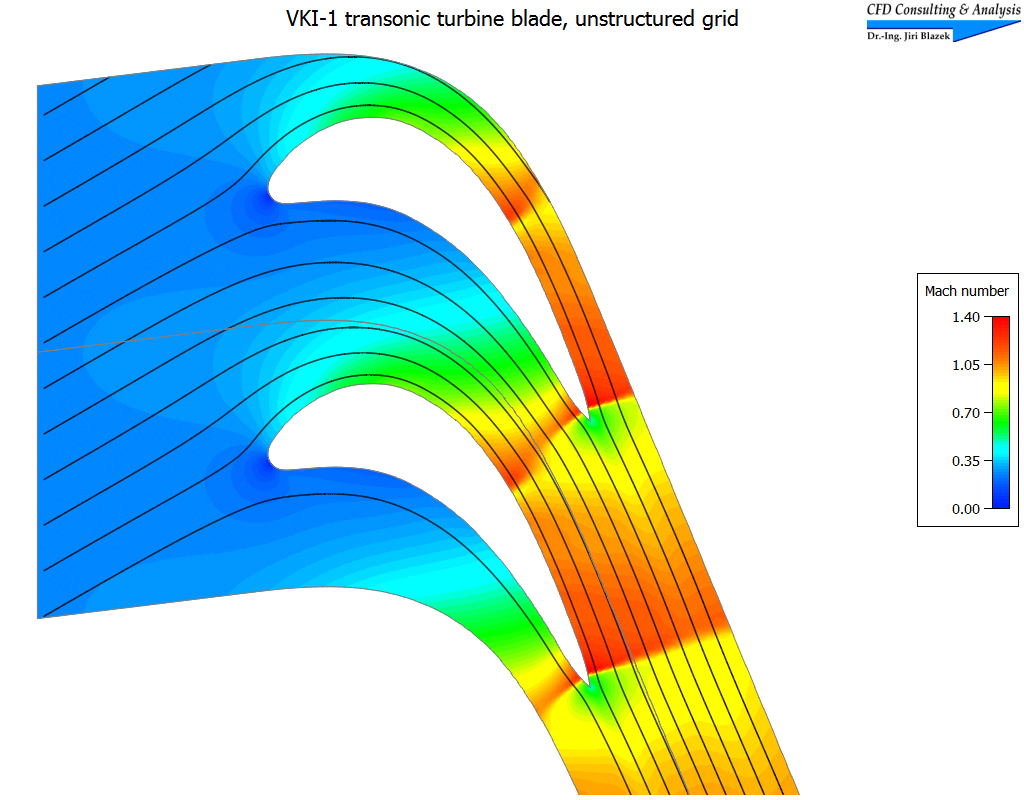
3. Transsonische Strömung im VKI-1 Turbinengitter

Die transsonische Gitterströmung wurde auf unstrukturiertem Netz bestehend aus 10.371 Dreiecken mit Hilfe des upwind Schemas von Roe simuliert. Die Bilder zeigen einen Ausschnitt zweier Netzteile (zusammengesetzt entlang des periodischen Randes), sowie Isolinien der Machzahl wie auch Stromlinien.

Zum Vergrößern anklicken

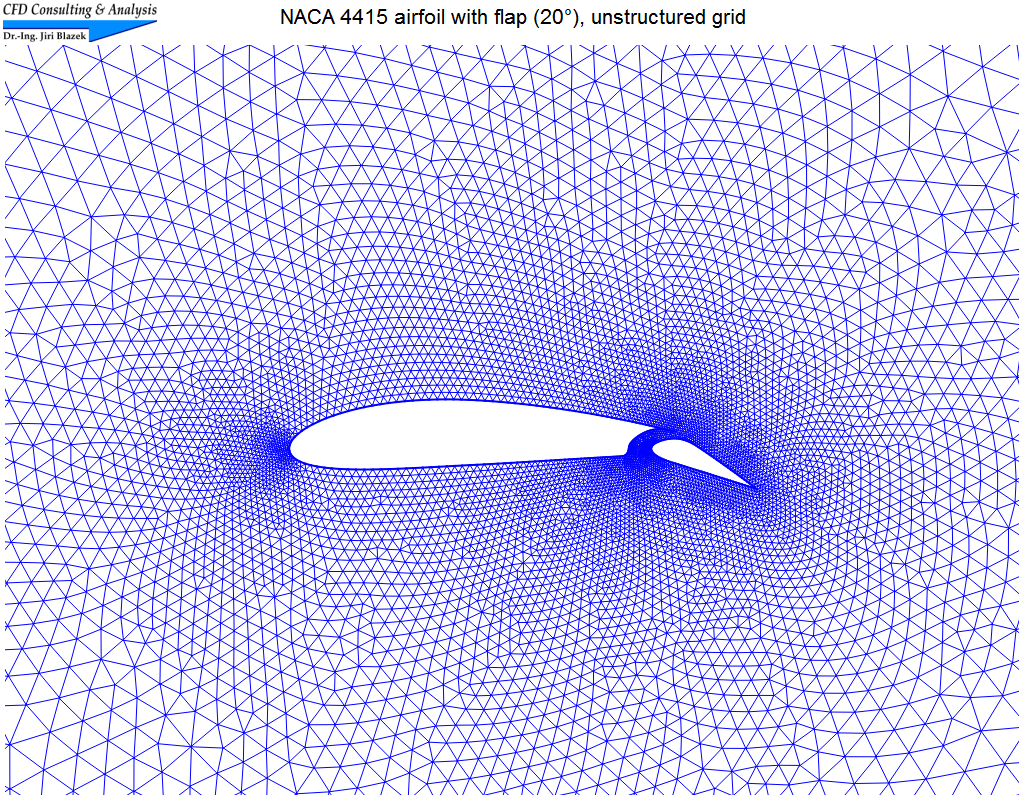
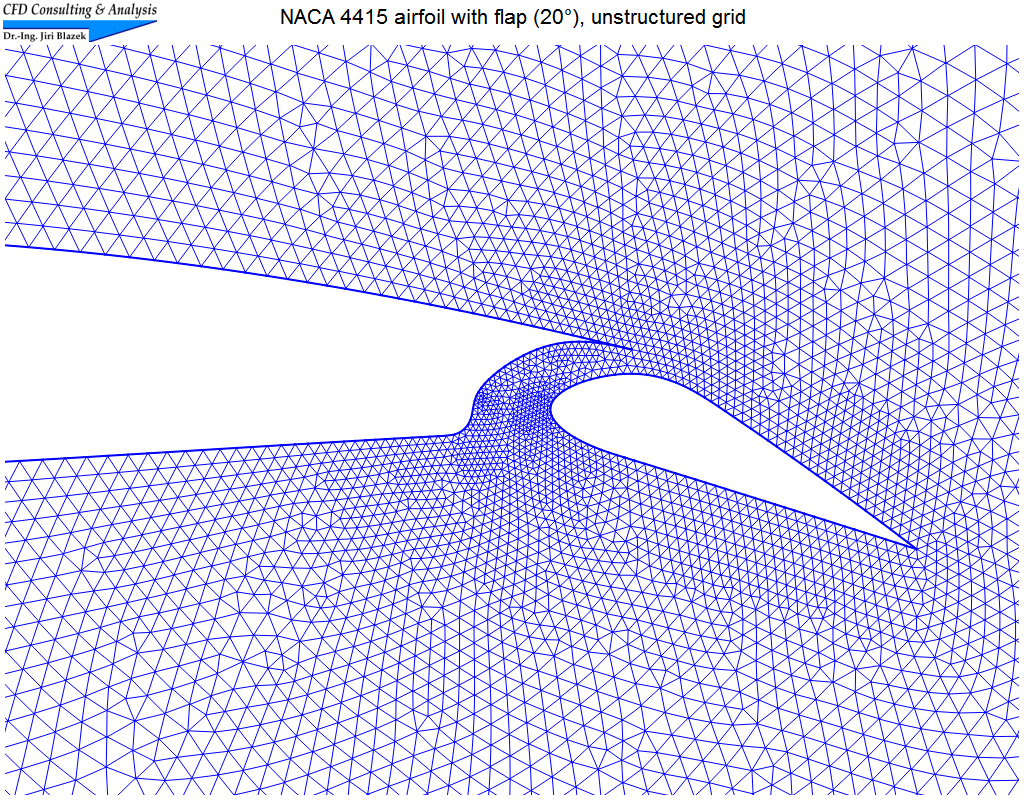
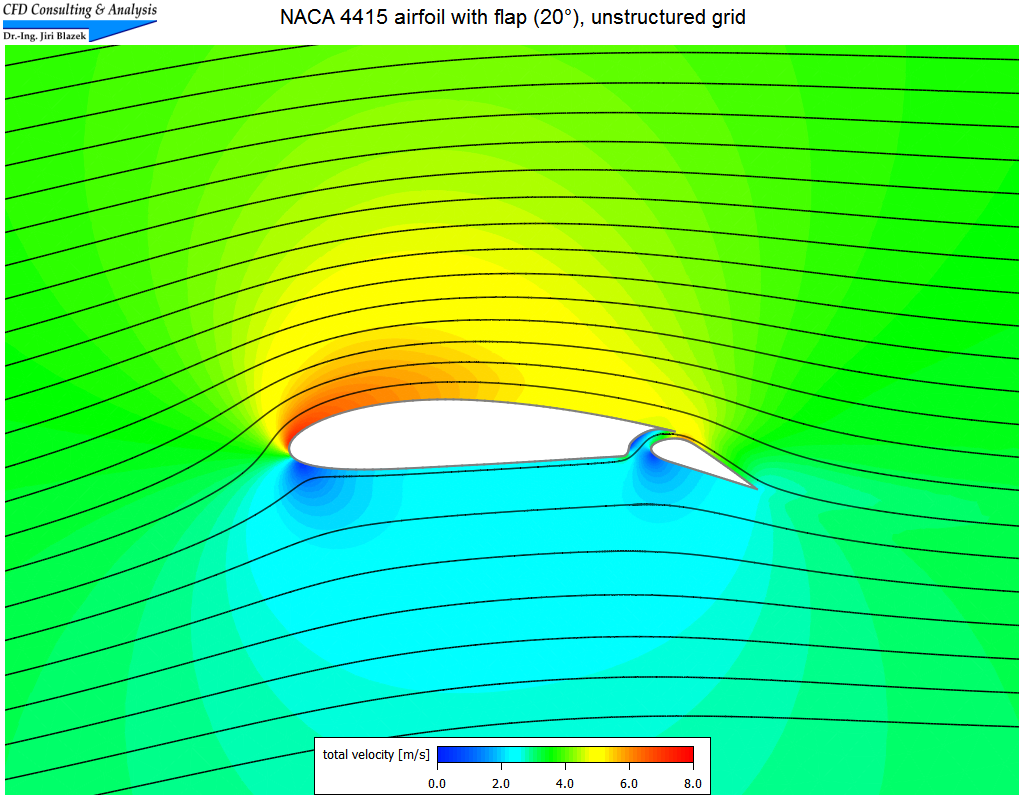
4. Unterschallströmung um ein Profil mit Klappe

Die nahezu inkompressible Strömung (Machzahl=0.01, α=5°) wurde auf unstrukturiertem Netz bestehend aus 20.413 Dreiecken mit Hilfe des upwind Schemas von Roe simuliert. Die Bilder zeigen Ausschnitte des Netzes, sowie Isolinien der Gesamtgeschwindigkeit wie auch Stromlinien.

Zum Vergrößern anklicken

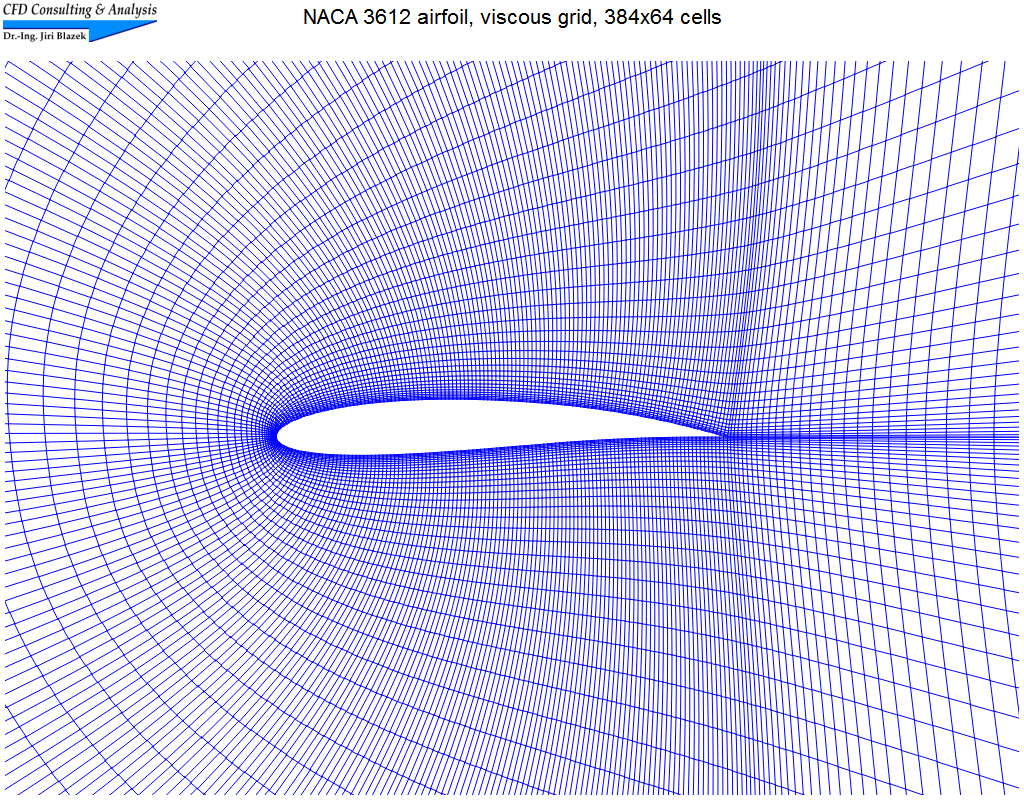
5. Viskose Unterschallströmung um ein Profil bei hohem Anstellwinkel

Die instationäre Strömung (Machzahl=0.2, α=30°) wurde wurde auf strukturiertem Netz (C-Typ) mit 384x64 Zellen mit Hilfe des upwind Schemas von Roe simuliert. Das Bild zeigt einen Teilausschnitt des Netzes. Im Video sind Geschwindigkeitsvektoren zu sehen, die entsprechend dem Wert der Gesamtgeschwindigkeit gefärbt sind.

Zum Vergrößern anklicken