Computational Fluid Dynamics: Principles and Applications
The objective of this extended and updated 3rd edition is to provide university students with a solid foundation for understanding the numerical methods employed in today's CFD and to familiarize them with modern CFD codes by hands-on experience. It is also intended for engineers and scientists starting to work in the field of numerical flow simulation, as well as for those who develop or who apply CFD codes. Due to the detailed index, the text is well suited as a reference handbook too. Each chapter includes an extensive bibliography, which provides an excellent basis for further studies.
A companion website of Elsevier Science contains the sources of 1-D and 2-D Euler and Navier-Stokes flow solvers (structured and unstructured), as well as of basic grid generation programs. Further included are tools for Von Neumann stability analysis of 1-D model equations and examples of various parallelization techniques. The programs are written in Fortran90 and in C++ and are well documented. Although being kept reasonably simple, the 2-D flow solvers are capable of treating a large variety of flow problems, ranging from nearly incompressible to hypersonic flows and from airfoils over cascades to solid rocket engines. Several examples can be seen here.
For ordering information, see at the bottom of this page. List of corrections to the text and updates to the example codes are provided on the next page. To contact the author, please write to: info@cfd-ca.de.
Chinese translation of the 3rd edition is also available. It can be ordered following this link.
Contents:
AcknowledgmentsList of Symbols
Abbreviations
1 Introduction
2 Governing Equations
2.1 The Flow and its Mathematical Description
2.2 Conservation Laws
2.3 Viscous Stresses
2.4 Complete System of the Navier-Stokes Equations
3 Principles of Solution of the Governing Equations
3.1 Spatial Discretization
3.2 Temporal Discretization
3.3 Turbulence Modeling
3.4 Initial and Boundary Conditions
4 Structured Finite Volume Schemes
4.1 Geometrical Quantities of a Control Volume
4.2 General Discretization Methodologies
4.3 Discretization of the Convective Fluxes
4.4 Discretization of the Viscous Fluxes
5 Unstructured Finite Volume Schemes
5.1 Geometrical Quantities of a Control Volume
5.2 General Discretization Methodologies
5.3 Discretization of the Convective Fluxes
5.4 Discretization of the Viscous Fluxes
6 Temporal Discretization
6.1 Explicit Time-Stepping Schemes
6.2 Implicit Time-Stepping Schemes
6.3 Methodologies for Unsteady Flows
7 Turbulence Modeling
7.1 Basic Equations of Turbulence
7.2 First-Order Closures
7.3 Large-Eddy Simulation
8 Boundary Conditions
8.1 Concept of Dummy Cells
8.2 Solid Wall
8.3 Far-Field
8.4 Inlet/Outlet Boundary
8.5 Injection Boundary
8.6 Symmetry Plane
8.7 Coordinate Cut
8.8 Periodic Boundaries
8.9 Interface Between Grid Blocks
8.10 Flow Gradients at Boundaries of Unstructured Grids
9 Acceleration Techniques
9.1 Local Time-Stepping
9.2 Enthalpy Damping
9.3 Residual Smoothing
9.4 Multigrid
9.5 Preconditioning for Low Mach Numbers
9.6 Parallelization
10 Consistency, Accuracy and Stability
10.1 Consistency Requirements
10.2 Accuracy of Discretization Scheme
10.3 Von Neumann Stability Analysis
11 Principles of Grid Generation
11.1 Structured Grids
11.2 Unstructured Grids
12 Software Applications
12.1 Programs for Stability Analysis
12.2 Structured 1-D Grid Generator
12.3 Structured 2-D Grid Generators
12.4 Structured to Unstructured Grid Converter
12.5 Quasi 1-D Euler Solver
12.6 Structured 2-D Euler/Navier-Stokes Solver
12.7 Unstructured 2-D Euler/Navier-Stokes Solver
12.8 Parallelization
A Appendix
A.1 Governing Equations in Differential Form
A.2 Quasilinear Form of the Euler Equations
A.3 Mathematical Character of the Governing Equations
A.4 Navier-Stokes Equations in Rotating Frame of Reference
A.5 Navier-Stokes Equations Formulated for Moving Grids
A.6 Thin Shear Layer Approximation
A.7 Parabolized Navier-Stokes Equations
A.8 Axisymmetric Form of the Navier-Stokes Equations
A.9 Convective Flux Jacobian
A.10 Viscous Flux Jacobian
A.11 Transformation from Conservative to Characteristic Variables
A.12 GMRES Algorithm
A.13 Tensor Notation
Index
Title: Computational Fluid Dynamics: Principles and Applications (3rd edition)
Author: J. Blazek, Ph.D.
Publisher: Elsevier Science Ltd. (www.elsevier.com)
Published: March 2015
Form: Hardcover, 466 pages
ISBN: 978-0-08-099995-1
See also the website with the source codes at Elsevier Science. The book can be conveniently ordered there as well.
Example Results of the 2-D Flow Solvers
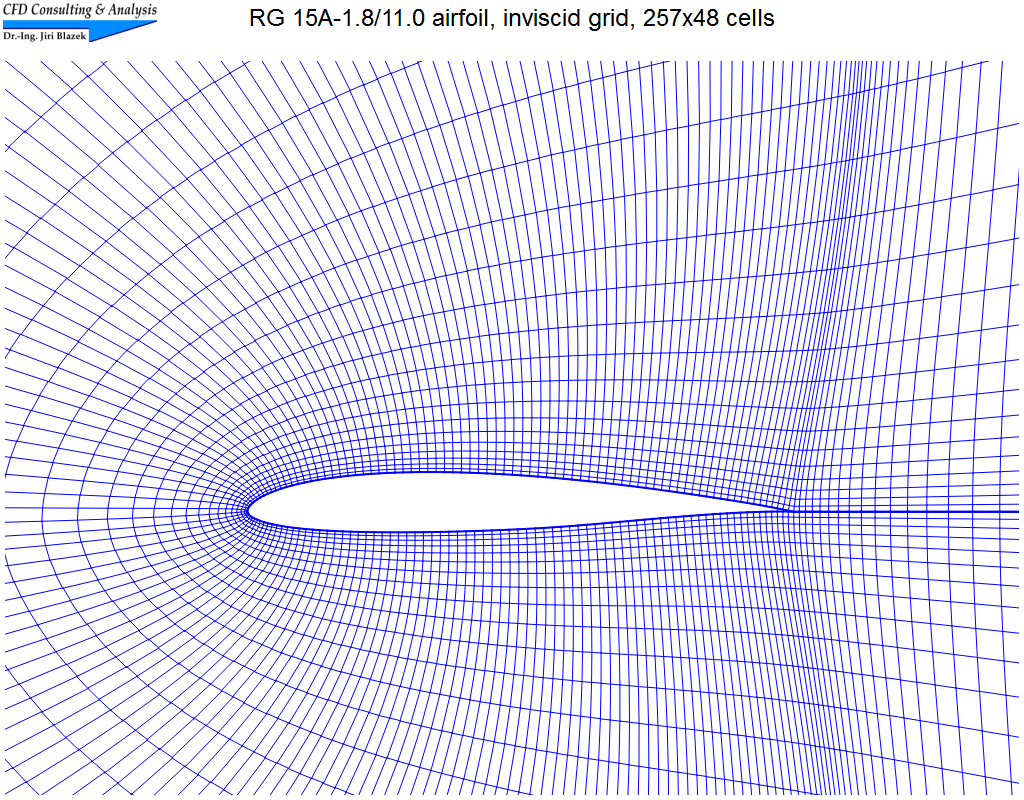
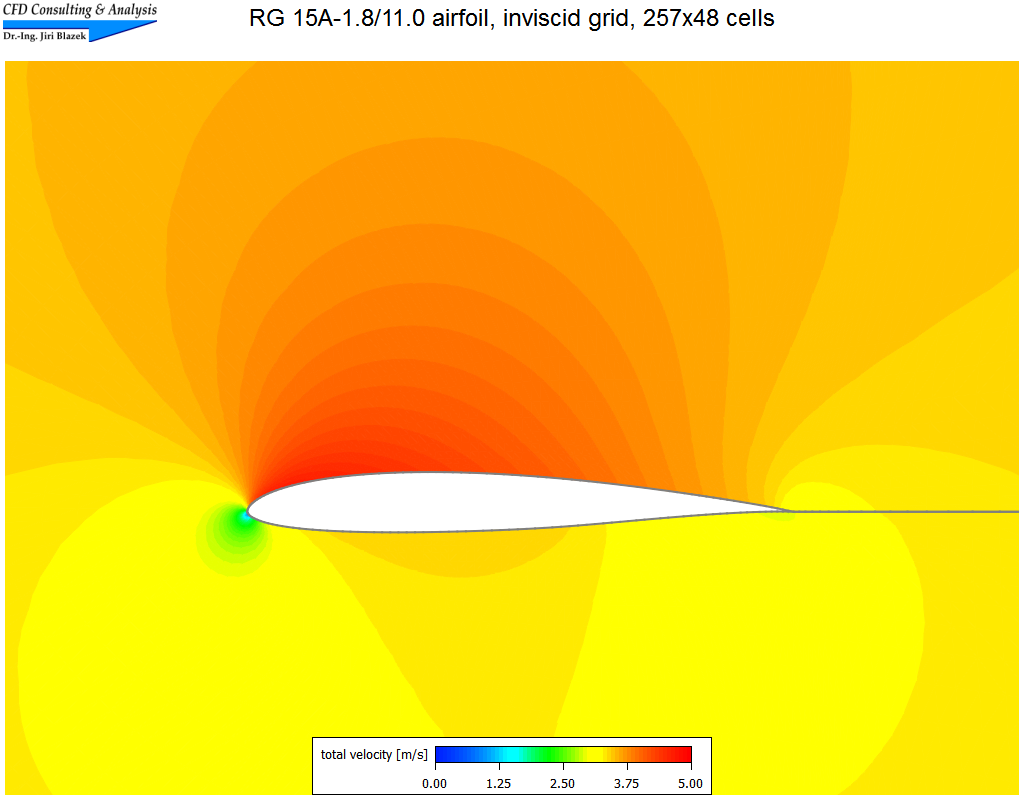
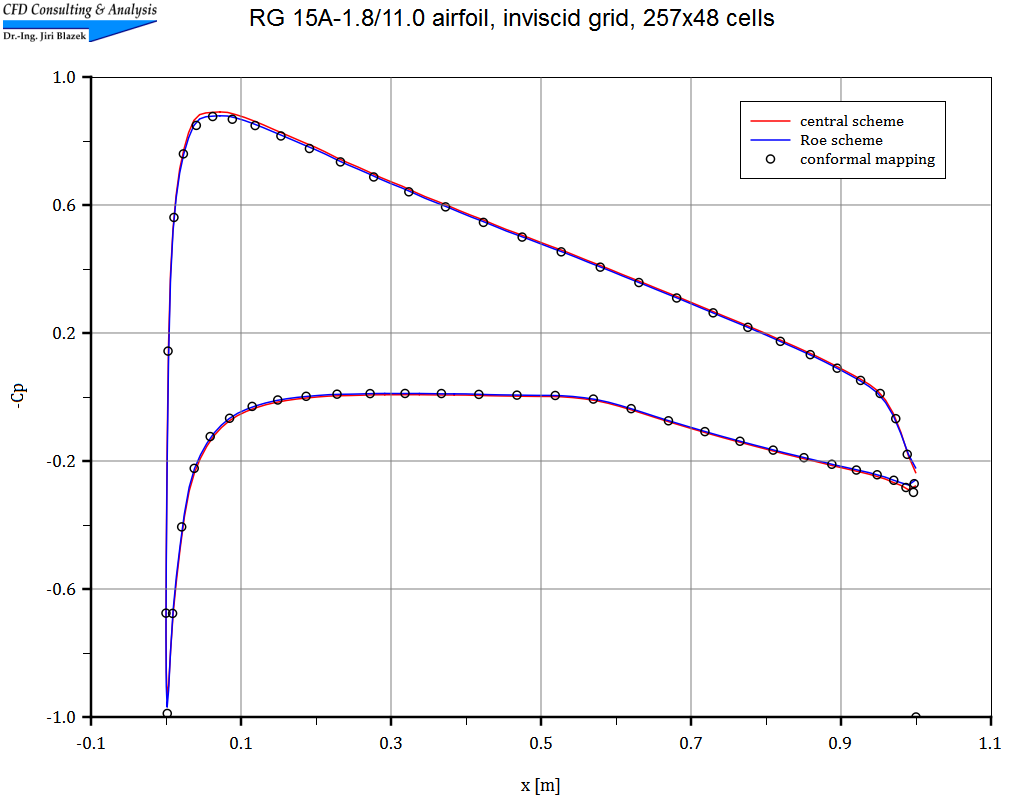
1. Subsonic flow past RG 15A-1.8/11.0 airfoil
The nearly incompressible flow (Mach=0.01, α=2°) was simulated on a structured grid (C-type) with 257x48 cells using the central, as well as Roe's upwind scheme. The pictures show a part of the grid, contours of the total velocity, and a comparison of the pressure coefficients.
Click to enlarge
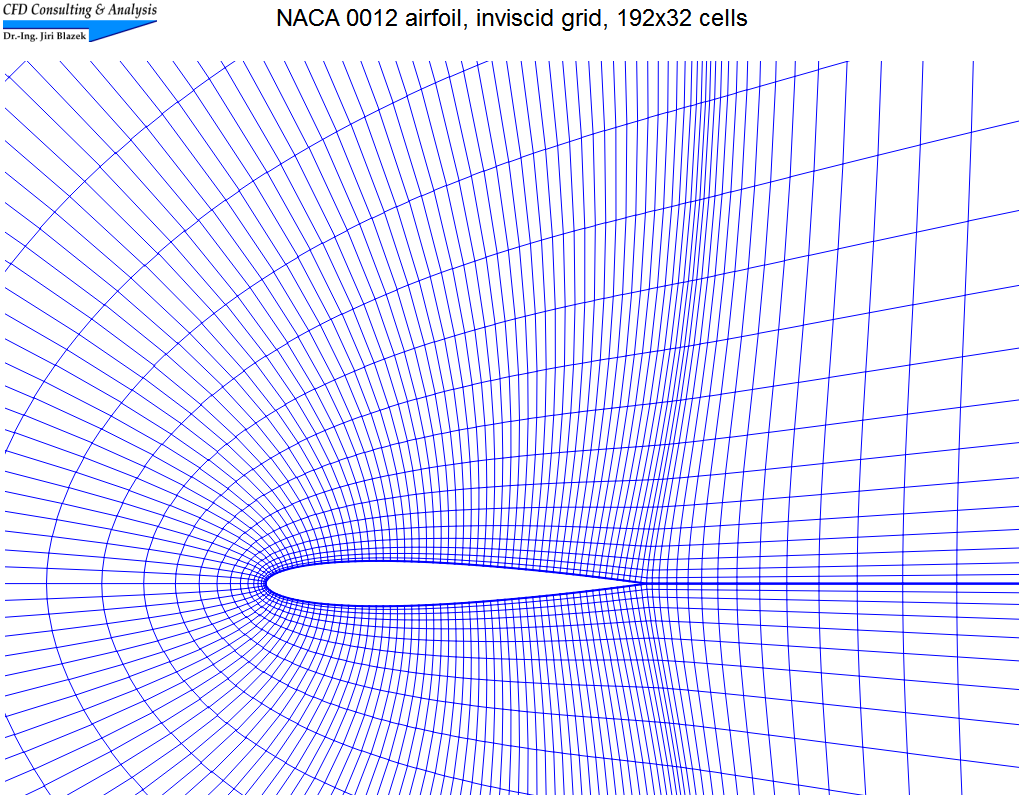
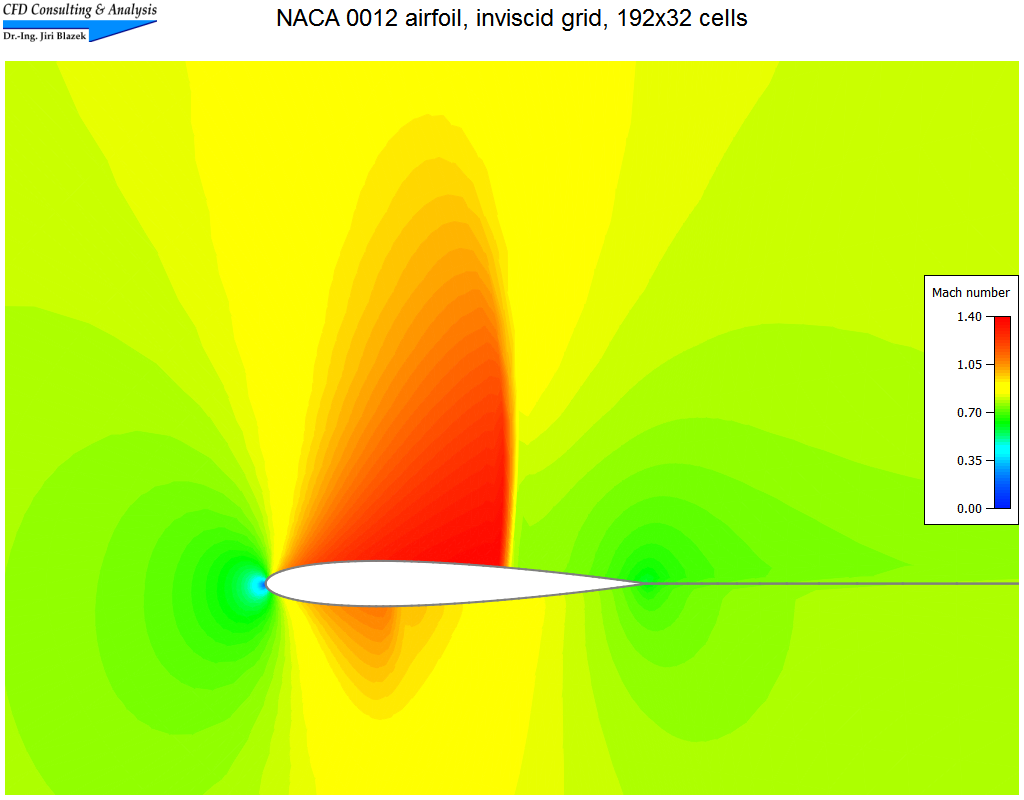
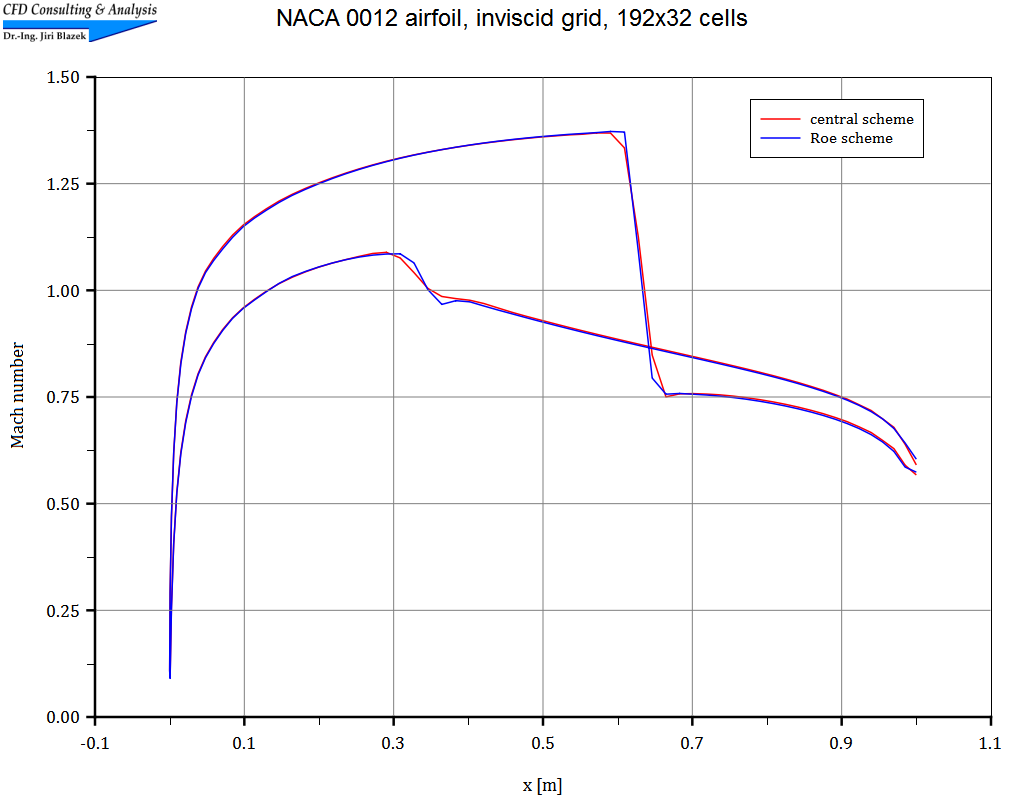
2. Transonic flow past NACA 0012 airfoil
The transonic flow (Mach=0.8, α=1.2°) was simulated on a structured grid (C-type) with 192x32 cells using both the central scheme and Roe's upwind scheme. The pictures show a part of the grid, contours of the Mach number, and a comparison of Mach-number distributions.
Click to enlarge
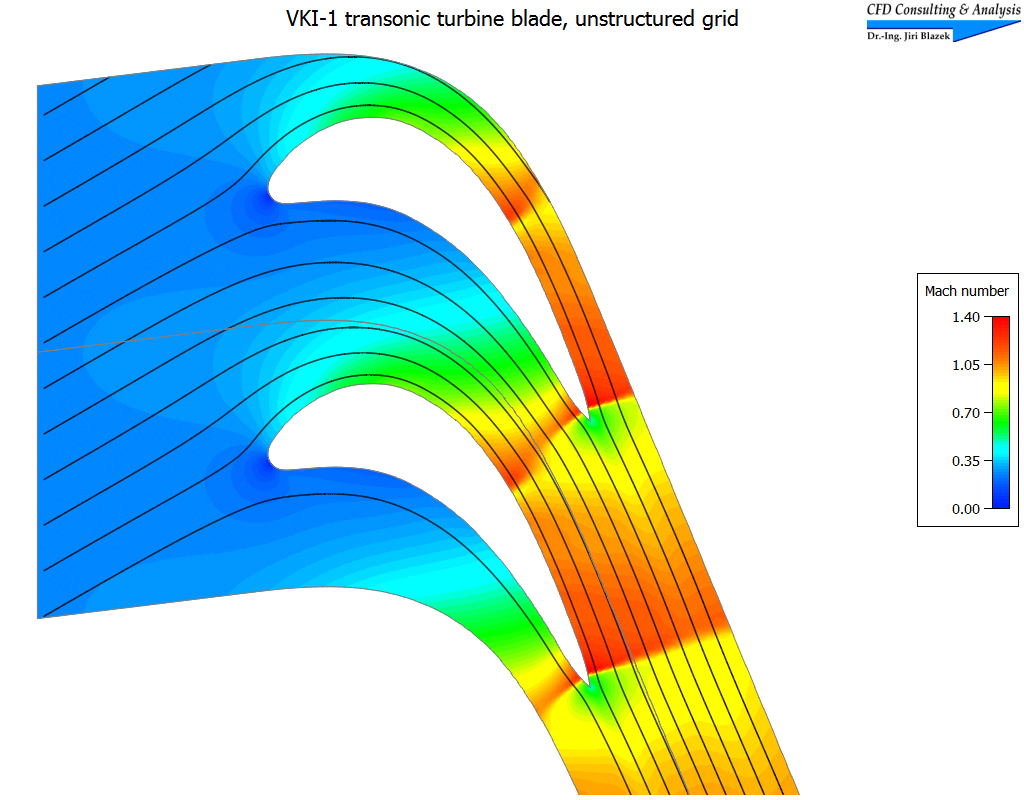
3. Transonic flow inside the VKI-1 turbine cascade
The flow inside the cascade was simulated on an unstructured triangular grid with 10'371 elements using Roe's upwind scheme. The pictures show a view of two grids joined at the periodic boundaries, as well as Mach contours overlaid by streamlines.
Click to enlarge
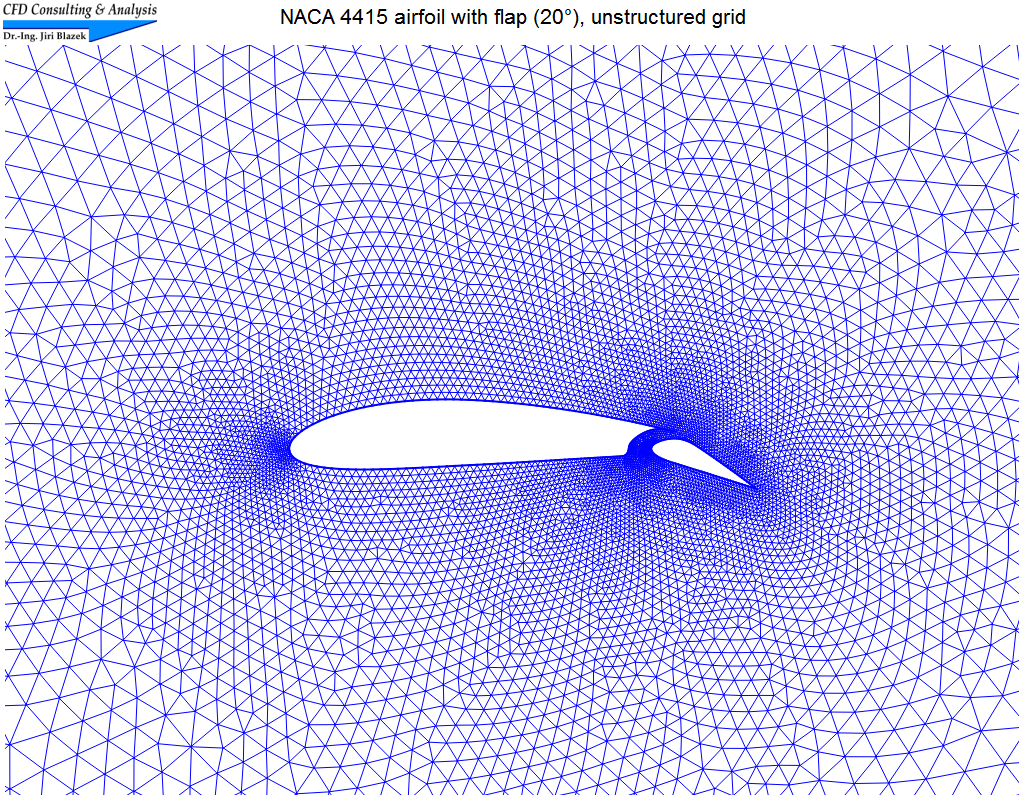
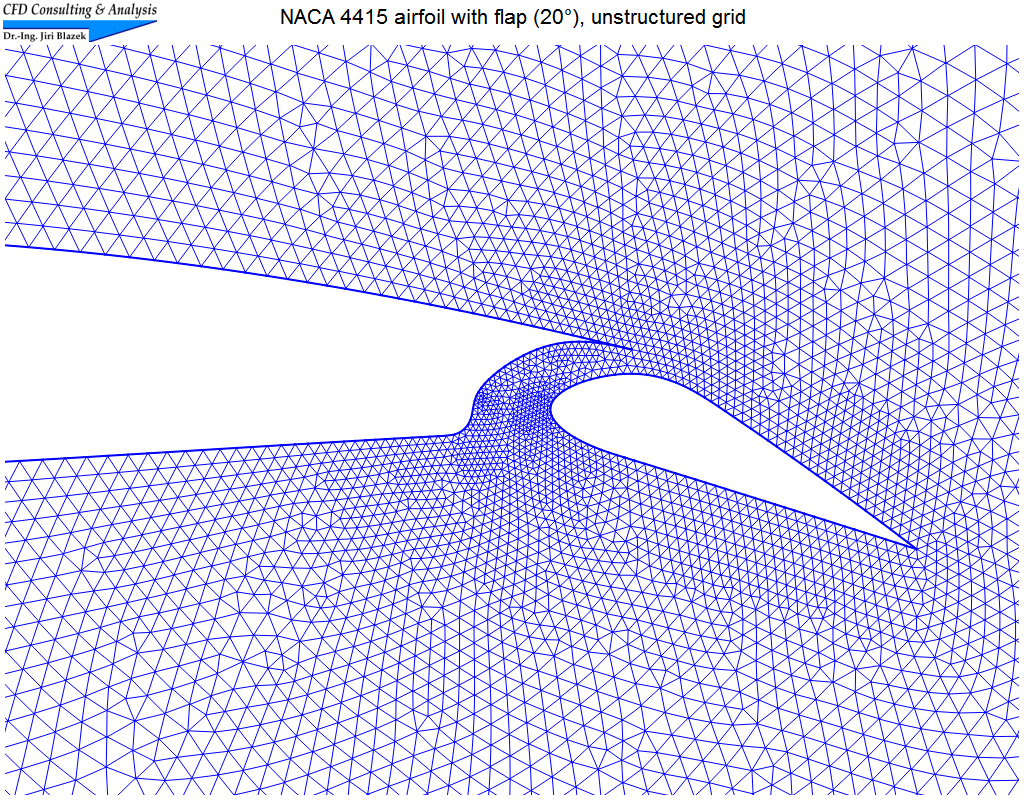
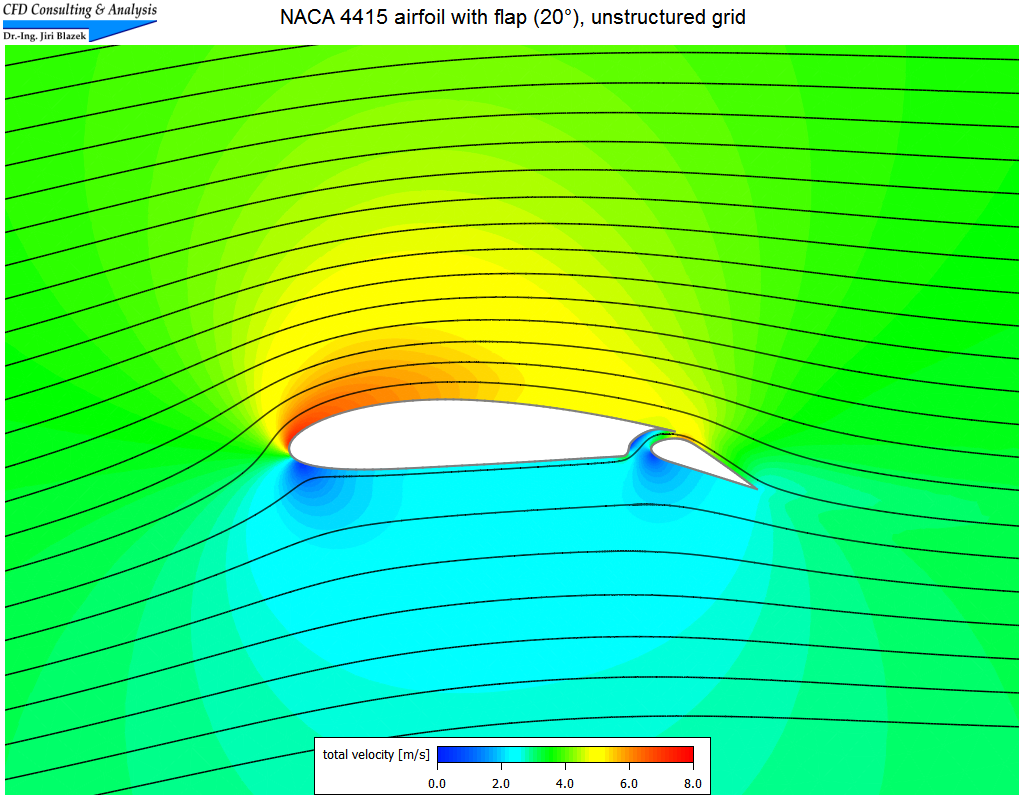
4. Subsonic flow past multi-element airfoil
The nearly incompressible flow (Mach=0.01, α=5°) was simulated on an unstructured triangular grid with 20'413 elements using Roe's upwind scheme. The pictures show parts of the grid and contours of the total velocity overlaid by streamlines.
Click to enlarge
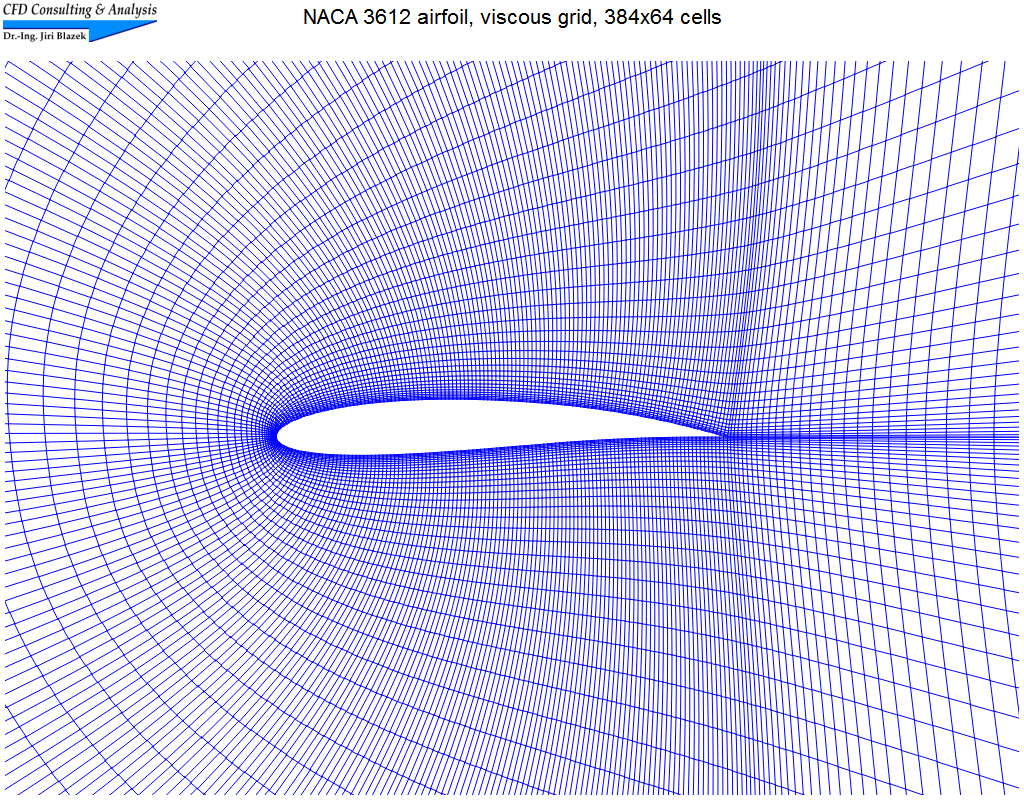
5. Subsonic viscous flow past airfoil at high angle of attack
The unsteady flow (Mach=0.2, α=30°) was simulated on a structured grid (C-type) with 384x64 cells using Roe's upwind scheme. The picture shows part of the grid, the video displays velocity vectors colored by the velocity magnitude.
Click to enlarge
© 2011-2024, CFD Consulting & Analysis. All rights reserved.